SOURCES OF NEUTRONS

There are several methods by which neutrons may be produced in the fuel cycle principle amongst these are:

Alpha Particle Induced Reactions
Plutonium and uranium isotopes decay by alpha particle emission. The alpha particle is absorbed by the nuclei of the low atomic number elements (Li, B, Be, O, F, C, Si, etc.) and a neutron is produced. The yield depends upon the chemical composition of the matrix and the alpha production rate for plutonium and uranium. Neutrons from (α,n) reactions are produced randomly (not time-correlated) and they exhibit a broad energy spectrum. Other α-emitting nuclides can also make important contributions, for example ²⁴¹Am.
Spontaneous Fission
The even-numbered isotopes of plutonium (²³⁸Pu, ²⁴⁰Pu, and ²⁴²Pu) spontaneously fission (SF) at a rate of 1100, 471, and 800 SF/gram-second respectively. Like (α,n) neutrons, SF neutrons have a broad energy spectrum. SF neutrons are time-correlated (several neutrons are produced at the same time), with the average number of neutrons per fission being between 2.16 and 2.26. Uranium isotopes and oddnumbered plutonium isotopes spontaneously fission at a much lower rate (0.0003 to 0.006 SF/gram-second). In spent fuel Cm and Cf isotopes may be significant.
Induced Fission
Fissions can be induced in ²³⁹Pu, ²³⁵U, and ²³⁸U by neutron interrogation of the sample with an external neutron source. Like SF neutrons, they have a broad energy spectrum and are time-correlated.

NEUTRON DETECTION

Neutrons have mass but no electrical charge. Because of this they cannot directly produce ionization in a detector, and therefore cannot be directly detected. This means that neutron detectors must rely upon a conversion process where an incident neutron interacts with a nucleus to produce a secondary charged particle. These charged particles are then directly detected and from them the presence of neutrons is deduced.

The most common reaction used for high efficiency thermal neutron detection today is:

where both the proton and the triton are detected by a gas filled proportional counters using ³He fill gas. Quench gas is also added to control the ionization process.

Another common method uses BF₃ filled detectors that utilize the fission of the ¹⁰B atom to provide the charged particle.

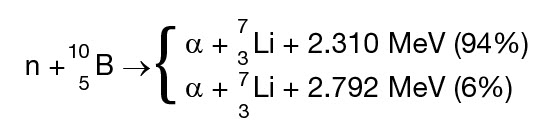
A typical instrument configuration that can be used with either of these detectors can be seen in Figure 1.48.

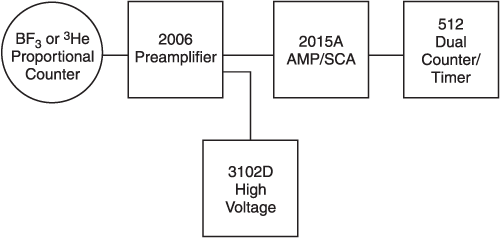
Figure 1.48 - Neutron Counter Electronics

Gas filled proportional counters offer low noise amplification of the ionization event producing a charge pulse processed by the attached nucleonics chain. They offer high detection efficiency with excellent gamma discrimination. They also provide a cost effective and stable means of constructing detectors for a wide range of applications.

Gas proportional detectors such as these are efficient only for thermal (low energy) neutrons; for high energy neutrons their capture cross sections are very small, making it very unlikely that a neutron will interact with the fill gas and cause the necessary detection reaction. Because of this it is necessary to slow the neutrons down to increase the probability of interaction.

This is usually done by surrounding the detector and/or the sample being counted by a hydrogen-rich material (moderator) such as high density polyethylene. Typically 10 cm (4 in.) of polyethylene surround the detector with a few cm being between the proportional counters and the neutron source.

The pulse height spectrum from the interaction of a thermal neutron in a typical ³He neutron detector will look as shown in Figure 1.49. Perhaps the most important point to note is there is no information about the primary neutron spectrum. Because all of the neutrons which are detected have been moderated to reduce their energy to the thermal level, all neutron energy information is lost. All of the events of interest fall into one peak, which is the reaction energy (765 keV). Once a discriminator has been set to eliminate the gamma interference and those events produced by interactions with the walls of the detector tube, simple gross counting is all that is required.

NEUTRON COINCIDENCE COUNTING

One of the more common applications of neutron detection and counting is the assay of fissile materials via the SF signature of the fertile nuclides. When the fissile material is contained in a high density matrix or a matrix which includes fission products, the interfering gammas from those fission products may very well overwhelm the weak gammas emitted from the fissile material, making neutron counting the only viable method available for performing the assay. In general neutron and gamma techniques are complementary. HRGS may provide relative isotopic information, for example, and the neutron assay bulk non destructive quantification.

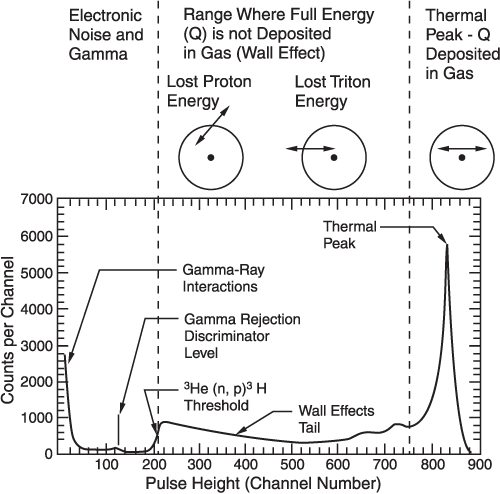
Figure 1.49 - Thermal Neutron Induced Pulse Height Spectrum from a Moderated ³He Detector

Unfortunately, for most assay needs, you cannot simply count all of the neutrons which are detected and from that result determine the amount of fissile material present in the sample. The radioactive decay of fissile material produces alpha particles which, in turn, produce neutrons via an (α,n) reaction with light elements within the sample matrix. For many materials of interest, the vast majority of the neutrons that are detected will be from the (α,n) reaction and not from the spontaneous fission of the fissile material.

It is not possible to use energy discrimination to distinguish neutrons from different sources, therefore, traditional spectroscopy techniques cannot be used. However, there is a characteristic time distribution difference between (α,n) neutrons and those neutrons produced as the result of a fission event that can be exploited. Specifically, fission events will produce multiple neutrons – usually two and sometimes three – simultaneously; (α,n) neutrons, on the other hand, are produced individually and randomly. This allows coincidence counting techniques to be used to distinguish the prompt fission neutrons from the random (α,n) neutrons.

A neutron coincidence system is shown schematically in Figure 1.50. The outputs from the ³He tubes are first processed by fast preamplifier/amplifier/discriminator (PAD) circuits, and logically ORed to the input of the neutron coincidence analyzer for processing.

The coincidence logic identifies those neutron counts that occur within a short time of each other: fission neutrons, closely spaced (α,n) neutrons, and counts due to “accidental coincidences”. Once one neutron has been detected, the probability of detecting another neutron from the same fission decreases approximately exponentially with time according to the following equation: P(t) = exp^(–t/td)
where:
P(t) = Probability of detecting coincidence neutrons in time t
t_d = die-away time of the moderated detector assembly

The die-away time is the characteristic time a neutron will survive before it is absorbed in the ³He tubes or escapes the counter. The neutron die-away time normally ranges from 10 to 128 µs depending upon the counter geometry.

The probability for detecting random neutrons from an item is constant with time. To determine whether the neutron events which are detected are time-correlated, two equal time periods are sampled by the coincidence logic for each neutron that is detected. The first gate or counting window is opened for a time period equal to about 1.267 t_d after a neutron is detected. Other counts within this time period are due to multiple fission neutrons from the triggering event, other fissions, and (α,n) reactions. After a delay of approximately 4000 µs, the second gate is opened and random neutron events are counted. The 4000 µs delay assures no time correlation with the neutron which triggered the count. The difference in the two timegated counts (Reals+Accidentals and Accidentals, respectively) is the net Real coincidence count, or Reals. The net Reals count is related to the fissile material in the sample by a calibration constant. Modern Mirion neutron analysis instruments are based on shift register counting. The shift register preserves the pulse sequence allowing coincidence data to be evaluated for each neutron event.

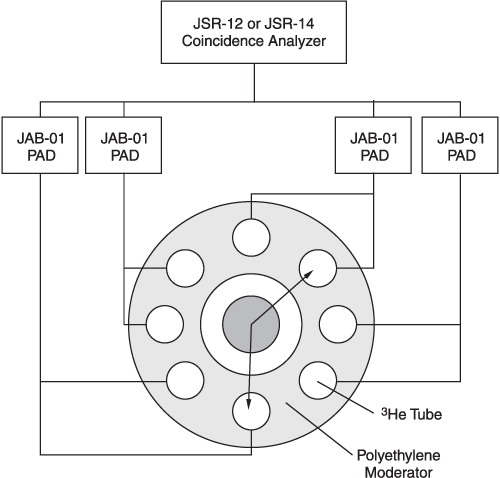
Figure 1.50 - Schematic Arrangement of a Thermal Well Coincidence Counter

MULTIPLICITY COUNTING

Neutron coincidence counting provides two measured values (Reals and Totals). In some cases, there are three (or more) unknown variables which need to be determined from the measurement. Typically these are: mass of ²⁴⁰Pu-effective (denoted m_eff), (α,n)-to-(SF,n) ratio (denoted α), and multiplication factor (denoted M or M_L). An example of this need is when impurities in the material under analysis preclude the estimation of the alpha ratio α from the typical isotopic method. In these cases, without a third measured parameter, some assumption has been made for the material and this can lead to large measurement biases or inaccuracies.

In Multiplicity Counting a third measured parameter is extracted from the distribution of the number of neutrons emitted in a spontaneous fission event (the multiplicity distribution). The three parameters are Singles, Doubles, and Triples, where Singles and Doubles are similar to Totals and Reals respectively, and Triples are the additional parameter derived. With three measured parameters, three unknowns may be calculated.

A special version of the shift register neutron coincidence analyzer performs the necessary data collection, and software reduces the histogram of multiplicity events recorded to Singles, Doubles and Triples event rates. These are used in conjunction with interpretational models to extract the unknown variables m_eff, α and M_L.

Although the primary use of multiplicity counting is for the measurement of samples without the need for assumptions on the material properties, there are other situations where multiplicity counting (and the extraction of a third parameter) can provide a benefit. For low level waste where M_L ~1, in addition to m_eff and α, the detection efficiency ε can also be extracted. This reduces the need for a careful evaluation of the detection efficiency for the measurement. Another application is the use of the measured multiplicity parameters in special algorithms that can be invoked to reduce detection limits and low-level bias caused by cosmic-ray induced spallation events in waste materials.

PASSIVE NEUTRON COUNTERS

When a neutron coincidence counter is used for the assay of ²³⁸Pu, ²⁴⁰Pu, and ²⁴²Pu, the neutrons from the spontaneous fission of these isotopes are detected and counted. Since no external neutron source is required to induce fission, assay systems of this type are known as Passive Neutron Counters.

ACTIVE NEUTRON COUNTERS

²³⁵U, ²³⁸U, and ²³⁹Pu do not spontaneously fission at a high enough rate to allow passive assay techniques to be used. For this reason, uranium assays utilize an external neutron source to induce fission in the sample. Assay systems using this technique are known as Active Neutron Counters. Various kinds exist; e.g. Active Well Coincidence Counter which makes use of Am Li sources; ²⁵²Cf shuffler; and the Differential Die Away techniques which uses a pulsed neutron generator. Mirion offers all of these methods and also undertakes special commissions.