Lab Experiment 5: Half-Life Measurement
Purpose:
- To demonstrate how to determine a half-life from decay data.
- To demonstrate the importance of background subtraction.
- To provide the theory on production of short-lived isotopes by neutron activation.
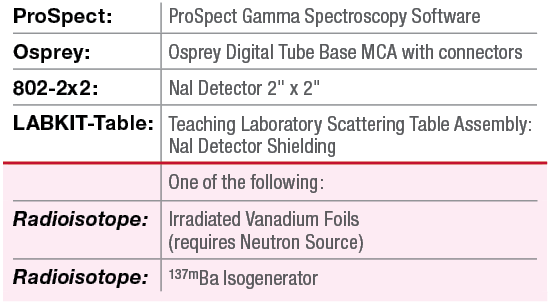
Equipment Required:
Theoretical Overview:

Nuclear half-life
The activity of a radioactive substance is the number of nuclei that decay (through the emission of particles) per unit time. The activity of radioactive material depends upon the amount of material present and decreases with time as the nuclei decay to another state. The change in the number of un-decayed nuclei, ΔN, is proportional to the number of un-decayed nuclei, N, and the time over which the change takes place, Δt:
![]()
where λ is the nuclear decay constant that depends on the particular isotope and the type of particle that is being emitted.
For infinitesimally small times this equation may be written as:
![]()
This can be solved using calculus to provide the following:
![]()
where:
N is the number of un-decayed nuclei at time t.
N0 is the number of un-decayed nuclide at time t = 0.
e is the natural exponential number (approximately equal to 2.7138).
Since the activity of a sample, A, is proportional to the number of nuclides, N, this can be expressed as:
![]()
where Ao is the initial activity of the sample at time t = 0. The activity of a sample can be measured as a function of time and the rate constant can be determined experimentally.
A useful parameter in nuclear measurement is the nuclear half-life. This is defined as the time that it takes the activity to decrease by half of the original activity. Measurement of the nuclear half-life for an unknown sample can help with sample identification through comparison of the measured value with published values.
The nuclear half-life τ is defined such that if the initial activity is Ao at time t = 0, then the activity at time t = τ will be A = ½Ao and:
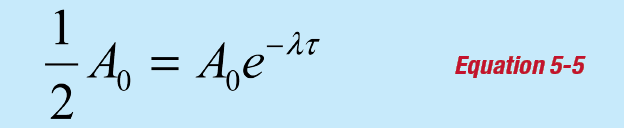
This equation is solved for the half-life by simplifying and taking the natural logarithm of both sides of the equation:

or:
![]()
Taking the natural logarithm of each side gives:
![]()
or:
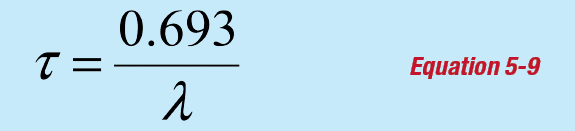
The figure below shows an example of 52V decay by measuring the counts observed as a function of time (following a subtraction of the background). The figure shows the exponential nature of the radioactive decay.
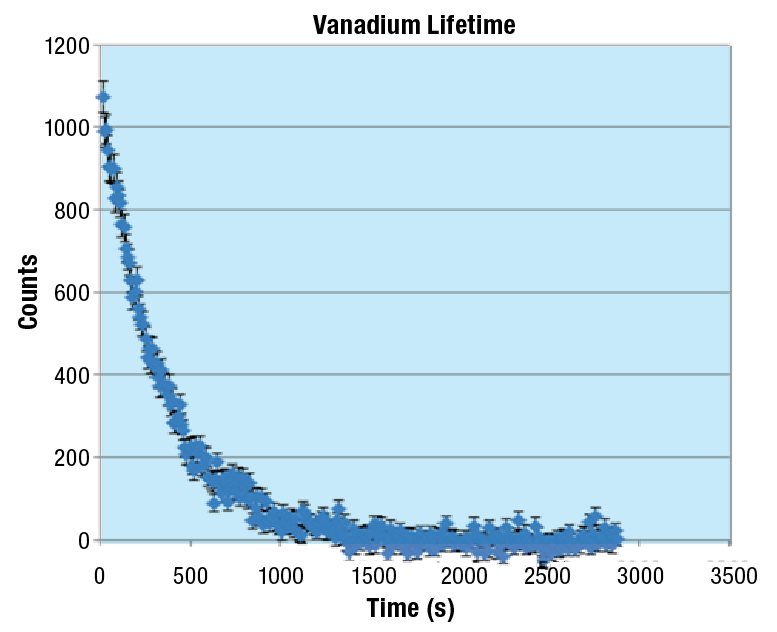
Figure 5-1: The observed counts of 52V with background subtraction as a function of time.
Neutron Activation
Equation 5-1 shows that the amount of decay (or emitted radiation) is proportional to the decay constant. Equation 5-9 demonstrates that this is inversely proportional to the half-life. This experiment therefore requires a nuclide with a short enough half-life to provide enough decay data in the relatively short duration of this teaching class.
A popular method of producing short-lived activity is to activate a natural metal (such as Vanadium) with a neutron source such as 252Cf or an Americium/Beryllium combined source.
To activate the sample, the Vanadium foil is placed in a water tank close to the neutron source (several centimeters away). The neutrons emitted by the source lose energy in the water. By the time they reach the sample the neutrons are known as “thermal neutrons” as their energy has reduced to the same energy as their surroundings, which is room temperature water. The energy of the neutrons is ~0.025 eV and the cross section for Vanadium to absorb these neutrons is 4.9 barns, which indicates a high probability for the reaction to occur.
Vanadium essentially consists on one isotope 51V (99.75% of natural vanadium). The foil absorbs the neutrons to produce 52V which decays by beta decay to 52Cr with a half-life of 3.75 minutes:
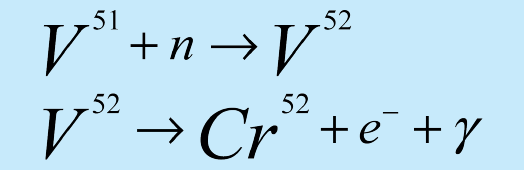
In this experiment, we will measure the gamma rays associated with the 52V decay in order to determine the half-life of 52V.
If a large neutron source and Vanadium foil are unavailable, an option is to purchase a 137mBa mini-generator. The generator utilizes the beta decay of 137Cs:
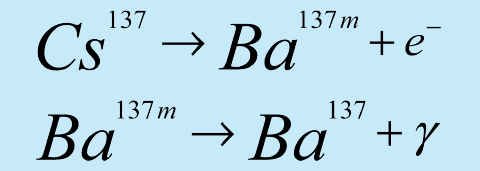
The parent isotope 137Cs beta decays with a half-life of 30.1 years to the metastable state of 137mBa. This further decays by gamma emission (662 keV) with a half-life of 2.6 min. to the stable 137Ba isotope. 137mBa is selectively "milked" from the generator, leaving behind the 137Cs parent. The generator can be used to measure the half-life of the 137mBa sample through measurement of the emitted 662 keV gamma rays.
Experiment 5 Guide:
1. Position the sample (irradiated vanadium foil or 137mBa sample) a few centimeters from the face of the NaI(Tl) detector.
2. Connect to the detector. Configure the MCA settings as recommended in Experiment 1.
3. Using the Acquisition tab, set the acquisition mode to MCS. Set the MCS conversion gain on the MCA tab to 256.
4. Set up the MCS acquisition such that the dwell time is 20s, the number of sweeps is 1 and the discriminator mode is 'Fast Discriminator'. Start the acquisition and stop it when the histogram is acquiring channel 60 (at an acquisition time of 20 minutes).
5. Save the data and then clear.
6. Remove the sample and repeat the measurement to acquire background data.
7. Export the sample and background data to Microsoft Excel or another spreadsheet application and subtract the background from the data.
8. Use Equation 5-4 to calculate the decay constant (and uncertainty). This will require plotting ln(A/A0 ) against t and determining the gradient (and uncertainty).
9. Use Equation 5-9 to calculate the half-life (and uncertainty). Compare this against published values.